大学物理

机械振动

简谐振动

定义: \(x(t) = Acos(\omega t+\varphi)\)

特征量:

振幅 \(A\)
周期 \(T\), 频率 \(v\), 角频率 \(\omega\). \(T=\frac{2\pi}{\omega}, v=1/T\)
相位 \(\omega t + \varphi\), 初相 \(\varphi\)
速度: \(v(t) = \frac{\mathrm{d}x}{\mathrm{d}t} = -\omega Asin(\omega t+\varphi), \varphi_v = \varphi + \frac{\pi}{2}\)
加速度: \(a(t) = \frac{\mathrm{d}v}{\mathrm{d}t} = -\omega^2Acos(\omega t+\varphi), \varphi_a = \varphi + \pi\)

同相: \(\Delta \varphi = \pm 2k\pi\), 两振动步调相同, 称为同相

反相: \(\Delta \varphi = \pm (2k+1)\pi\), 两振动步调相反, 称为反相

谐振子

受线性回复力 \(F=-kx\)

动力学方程:

\[ F=-kx=ma \Rightarrow \frac{\mathrm{d}^2x}{\mathrm{d}t^2} + \omega^2x = 0 \Rightarrow x(t) = Acos(\omega t+\varphi) \\ \omega = \sqrt{\frac{k}{m}} \]

由初始条件确定的量:

\[ x = Acos(\omega t+\varphi) \Rightarrow x_0 = Acos(\varphi), v_0 = -\omega Asin(\varphi) \\ A = \sqrt{x_0^2 + \frac{v_0^2}{\omega^2}}, \varphi = arctan(-\frac{v_0}{\omega x_0}) \]

能量

动能

\[ E_k = \frac{1}{2}mv^2=\frac{1}{2}kA^2sin^2(\omega t+\varphi) \\ E_{max}=\frac{1}{2}kA^2, E_{min}=0, \overline{E_k} = \frac{1}{T}\int_t^{t+T}E_k\mathrm{d}t = \frac{1}{4}kA^2 \]

势能

\[ E_p = \frac{1}{2}kx^2=\frac{1}{2}kA^2cos^2(\omega t+\varphi) \\ E_{max}=\frac{1}{2}kA^2, E_{min}=0, \overline{E_p} = \frac{1}{T}\int_t^{t+T}E_p\mathrm{d}t = \frac{1}{4}kA^2 \]

机械能 (守恒)

\[ E = E_k + E_p = \frac{1}{2}kA^2 \]

简谐振动的合成

同方向同频率

\[ x_1 = A_1cos(\omega t+\varphi_1),\ x_2 = A_2cos(\omega t+\varphi_2) \\ x = x_1 + x_2 = Acos(\omega t+\varphi) \\ A = \sqrt{A_1^2 + A_2^2 + 2A_1A_2cos(\varphi_1-\varphi_2)}, \varphi = arctan(\frac{A_1sin\varphi_1+A_2sin\varphi_2}{A_1cos\varphi_1+A_2cos\varphi_2}) \]

同频率简谐振动的合运动仍是简谐振动

同方向不同频率振幅相同

\[ x_1 = Acos\omega_1 t,\ x_2 = Acos\omega_2 t \\ x = x_1 + x_2 = 2Acos\frac{\omega_1-\omega_2}{2}t \cdot cos\frac{\omega_1+\omega_2}{2}t \]

\(A(t) = 2Acos\frac{\omega_1-\omega_2}{2}t\) 随 \(t\) 缓变, \(cos\bar\omega t = cos\frac{\omega_1+\omega_2}{2}t\) 随 \(t\) 快变

此时可以视为振幅缓变的简谐振动

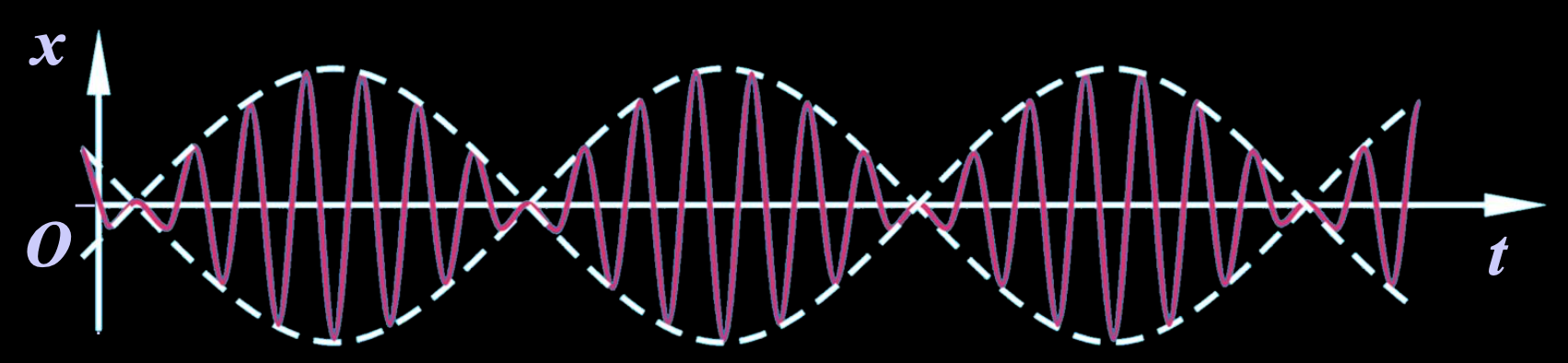
Simple harmonic vibration with slowly varying amplitude

垂直方向同频率

\[ x = A_1cos(\omega t + \varphi_1),\ y = A_2cos(\omega t + \varphi_2) \\ \frac{x^2}{A_1^2} + \frac{y^2}{A_2^2} - 2\frac{x}{A_1}\frac{y}{A_2}cos(\varphi_1-\varphi_2) = sin^2(\varphi_1-\varphi_2) \]

当 \(\Delta \varphi = k\pi\) 时, \(\frac{x}{A_1} \pm \frac{y}{A_2} = 0\), 运动轨迹为直线
当 \(\Delta \varphi = k\pi + \frac{\pi}{2}\) 时, 运动轨迹为圆
其余情况, 运动轨迹为椭圆
垂直方向不同频率

振动频率为整数比时, 成周期性运动, 振动轨迹为闭合曲线, 称为Lissajous图

阻尼振动

阻尼力 \(f = -\mu \dot{x}\)

微分方程(以弹簧振子为例):

\[ m\ddot{x} = -kx-\mu\dot{x} \Rightarrow \ddot{x} + 2n\dot{x} + \omega_0^2x = 0 \\ \omega_0 = \sqrt{\frac{k}{m}}, n = \frac{\mu}{2m} \]

\(n\) 称为阻尼系数

振动方程 - 小阻尼 (\(n^2 < \omega_0^2\))

\[ x = Ae^{-nt}cos(\sqrt{\omega_0^2 - n^2} t+\varphi) \]

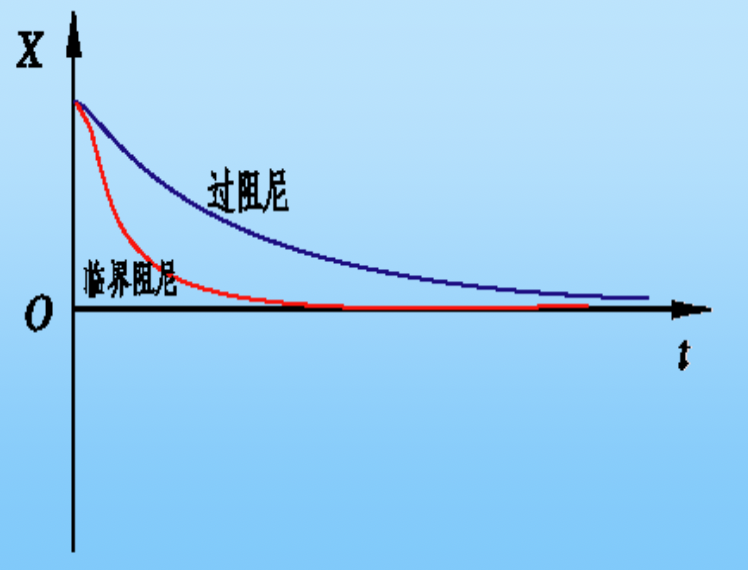
临界阻尼 (\(n^2 = \omega_0^2\))
过阻尼 (\(n^2 > \omega_0^2\))

在过阻尼和临界阻尼, 不发生振动

Overdamping and critical damping

受迫振动

周期性策动力: \(F=F_0cos\omega t\)

微分方程

\[ m\ddot{x} = -kx - \mu\dot{x} + F_0cos\omega t \Rightarrow \ddot{x} + 2n\dot{x} + \omega_0^2x = fcos\omega t \\ \omega_0 = \sqrt{\frac{k}{m}}, n = \frac{\mu}{2m}, f = \frac{F_0}{m} \]

稳态解为 \(x=Acos(\omega t - \varphi)\), 带回原微分方程即可求得振幅及初相

\[ A = \frac{f}{\sqrt{(\omega_0^2-\omega^2)^2 + 4n^2\omega^2}}, tan\varphi = \frac{2n\omega}{\omega_0^2-\omega^2} \]

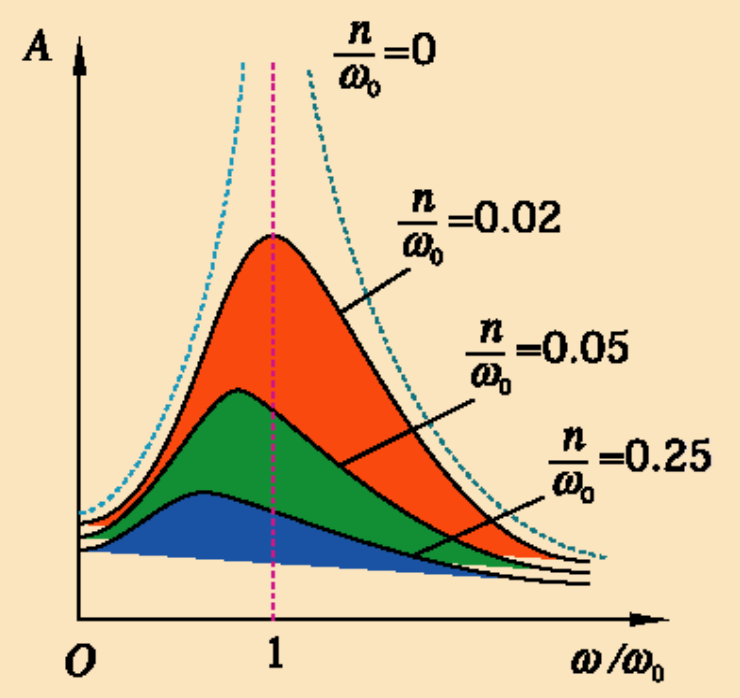
结论: 受迫振动振幅 \(A\) 及受迫振动与驱动力的相位差\(\varphi\) 均与初始条件无关

特殊情况:

位移共振 (振幅取极值)

共振频率: \(\omega_r = \sqrt{\omega_0^2 - 2n^2}\)

共振振幅: \(A_r = \frac{f}{2n\sqrt{\omega_0^2 - n^2}}\)

amplitude resonance curve

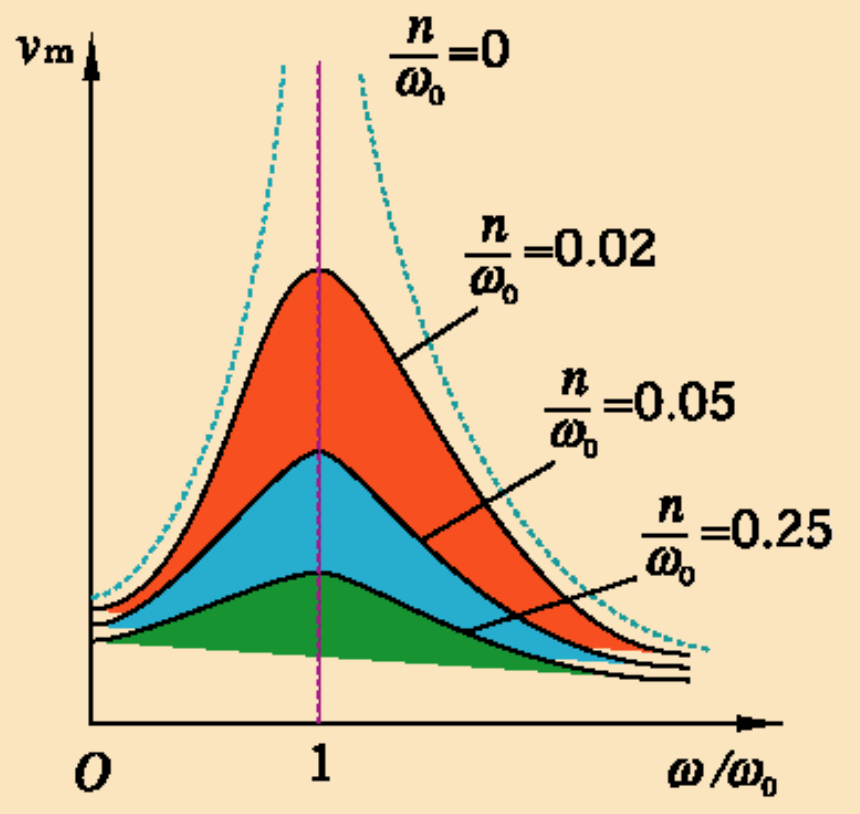
速度共振 (速度振幅 \(\omega A\) 取极值)

共振频率: \(\omega = \omega_0\)

共振速度振幅: \(v_m = \frac{f}{2n}\)

\(tan \varphi \to \infin \Rightarrow \varphi = \frac{\pi}{2}\)

此时,速度与策动力同相, 策动力总做正功, 向系统输入能量最大

velocity resonance curve

非谐振动的傅立叶分解

任何周期性运动都可以分解为一系列简谐振动的叠加

\[ x = \sum_{n=1}^{\infin}A_n cos(n\omega t + \varphi_n) \]

机械波

机械波的产生

弹性介质的弹性形变在空间中传播, 机械波是振动状态(相位)的传播

波源: 产生机械振动的物体
弹性介质: 承担机械振动的物体

类型: - 纵波: 振动方向与波的传播方向平行, 如空气中的声波 - 横波: 振动方向与波的传播方向垂直, 如柔绳上的绳波

气体和液体内只能传播纵波, 不能传播横波

波的几何描述

波面: 在传播过程中, 任一时刻, 振动相位相同的点的集合

波线: 沿波的传播方向, 所作的有方向的线

在各向同性均匀介质中, 波面 \(\perp\) 波线

波的特征物理量

波长 \(\lambda\): 波源做一次完全振动, 波前进的距离, 反映波的空间周期性
周期 \(T\): 波在介质中传播一个波长所需的时间, 反映波的时间周期性
频率 \(v\): 单位时间内, 波源振动的次数. \(v = 1/T\)
波速 \(u\): 波在介质中传播的速度. \(u = \frac{\lambda}{T} = v \lambda\)

说明: - 波的周期与频率是波源的固有属性, 与介质无关 - 波速与介质的性质有关, 与波源无关

平面简谐波

\[ y_0 = f(t) \Rightarrow y = f(t - \frac{x}{u}) = f(x, t) \\ y_0 = A cos(\omega t + \varphi) \Rightarrow y = A cos(\omega (t - \frac{x}{u}) + \varphi) \]

物理意义:

振动状态的空间周期性: \(y(x+\lambda, t) = y(x, t)\)
波形传播的时间周期性: \(y(x, t+T) = y(x, t)\)
\(x\) 给定, \(y = y(t)\) 是 \(x\) 处的振动方程
\(t\) 给定, \(y = y(x)\) 是 \(t\) 时刻的波形方程

波动微分方程:

\[ y(x, t) = A cos(\omega (t - \frac{x}{u}) + \varphi_0) \Rightarrow \\ \frac{\partial^2y}{\partial t^2} = -\omega^2Acos(\omega (t - \frac{x}{u}) + \varphi_0),\ \ \frac{\partial^2y}{\partial x^2} = -\frac{\omega^2}{u^2}Acos(\omega (t - \frac{x}{u}) + \varphi_0) \Rightarrow \\ \frac{\partial^2y}{\partial x^2} = \frac{1}{u^2}\frac{\partial^2y}{\partial t^2} \]

该微分方程描述了一切平面波, 更通用的形式为

\[ \nabla^2\xi=\frac{1}{u^2}\frac{\partial^2\xi}{\partial t^2} \]

波的能量

以绳索上传播的横波为例, 取线元 \(\mathrm{d} m = \mu \mathrm{d}x\), \(T=u^2\mu\)

\[ \begin{aligned} 动能:\ & W_k=\frac{1}{2}\mathrm{d} m v^2=\frac{1}{2}\mu\mathrm{d}x\left(\frac{\partial y}{\partial t}\right)^2=\frac{1}{2}\mu\mathrm{d} xA^2\omega^2sin^2(\omega (t-\frac{x}{u})+\varphi) \\ &\mathrm{d} l = \sqrt{(\mathrm{d} x)^2 + (\mathrm{d} y)^2} = \mathrm{d} x\sqrt{1+\left(\frac{\partial y}{\partial x}\right)^2} = \mathrm{d} x\left(1+\frac{1}{2}\left(\frac{\partial y}{\partial x}\right)^2\right) \\ 势能:\ & W_p = T(\mathrm{d} l - \mathrm{d} x) = \frac{1}{2}T\mathrm{d} x\left(\frac{\partial y}{\partial x}\right)^2 = \frac{1}{2}\mu\mathrm{d} xA^2\omega^2sin^2(\omega (t-\frac{x}{u})+\varphi) \\ 机械能:\ & W_k=W_p,\ W=W_k+W_p=\mu\mathrm{d} xA^2\omega^2sin^2(\omega (t-\frac{x}{u})+\varphi) \\ 能量密度:\ & w=\frac{\mathrm{d} W}{S\mathrm{d} x}=\rho A^2\omega^2sin^2(\omega (t-\frac{x}{u})+\varphi) \\ 能流密度:\ & \vec{J}=w\vec{u} \\ 平均能量密度:\ & \overline{w}=\frac{1}{T}\int_0^Tw\mathrm{d} t=\frac{1}{2}\rho A^2\omega^2 \\ 平均能流密度:\ & I=\overline{J}=\overline{w}u=\frac{1}{2}\rho A^2\omega^2u \end{aligned} \]

惠更斯原理

波面的每一点可以认为是产生球面次波的点波源，而以后任何时刻的波面则可看作是这些次波的包络。

波的干涉

波传播的独立性: 当几列波在传播过程中相遇时, 每列波的传播都不受其他波的影响, 仍保持原来的传播状态

叠加原理: 波的振动效果等于各个波的振动效果的矢量和

干涉现象: 当两列相干波叠加时, 其合振幅形成一种稳定分布

相干条件: 频率相同, 振动方向相同, 相位差恒定

\[ \begin{aligned} & y_{01} = A cos(\omega t + \varphi_1),\ y_{02} = A cos(\omega t + \varphi_2) \\ 光程差:\ & \delta = r_2 - r_1 \\ 相位差:\ & \Delta\varphi = \varphi_2 - \varphi_1 - 2\pi\frac{\delta}{\lambda} \\ 振幅:\ & A^2 = A_1^2 + A_2^2 + 2A_1A_2cos\Delta\varphi \\ 波的强度:\ & I = I_1 + I_2 + 2\sqrt{I_1I_2}cos\Delta\varphi \end{aligned} \]

当 \(\Delta\varphi=\pm 2k\pi\) 时, \(A_{max} = A_1 + A_2,\ I_{max} = I_1 + I_2 + \sqrt{I_1I_2}\), 干涉相长

当 \(\Delta\varphi=\pm(2k+1)\pi\) 时, \(A_{min} = |A_1 - A_2|,\ I_{min} = I_1 + I_2 - \sqrt{I_1I_2}\), 干涉相消

驻波

两列等振幅相干波相向传播时叠加形成驻波

形成条件: \(L=n\frac{\lambda}{2}\)

波函数:

\[ y_1 = Acos2\pi(vt-\frac{x}{\lambda}), y_2 = Acos2\pi(vt+\frac{x}{\lambda}) \\ y = y_1 + y_2 = 2Acos2\pi \frac{x}{\lambda}\cdot cos 2\pi vt \]

\(A'(x) = 2Acos2\pi\frac{x}{\lambda}\), 各质点振幅按余弦分布

波腹 (\(A'=A'_{max}\)): \(\left|cos\frac{2\pi x}{\lambda}\right|=1, x=k\frac{\lambda}{2}\)

波节 (\(A'=A'_{min}\)): \(\left|cos\frac{2\pi x}{\lambda}\right|=0, x=k\frac{\lambda}{2}+\frac{\lambda}{4}\)

相邻两波腹、波节间距均为 \(\frac{\lambda}{2}\) .

此时, 能量仅在波腹与波节间传播, 不发生能量定向传播, 因此称为"驻"波

半波损: 入射波从波疏介质向波密介质传播, 反射点入射波与反射波反相

多普勒效应

观察者、波源相对介质运动, 波源发出的波的频率与观察者所测得的波的频率不同

以下分析, 统一取相互靠近方向为正

波源静止, 观察者运动

\[ f = \frac{u+v_0}{\lambda}=\frac{u+v_0}{u/f_0}=(1+\frac{v_0}{u})f_0 \]

观察者静止, 波源运动

\[ \lambda'=\lambda-v_sT=uT-v_sT=\frac{u-v_s}{f_0} \Rightarrow \\ f=\frac{u}{\lambda'}=\frac{u}{u-v_s}f_0 \]

波源、观察者均运动

\[ f=\frac{u+v_0}{\lambda-v_sT}=\frac{u+v_0}{u-v_s}f_0 \]

最后更新: October 27, 2023
创建日期: October 27, 2023