跳转至

复杂网络动力学

绪论

复杂网络指具有复杂拓扑结构和动力学行为的大规模网络.

主要特征:

  • 稀疏性: 具有 \(N\) 个节点的网络, 连接数通常为 \(O(n)\), 而非 \(O(n^2)\)
  • 小世界特性: 平均路径长度 \(L\) 较短
  • 无标度特性: 节点度分布 \(P(k)\) 服从幂律分布, 与系统特征长度无关.

复杂网络的基本概念

度 \(k\), 平均度 \(<k>\), 度分布函数 \(P(k)\), 聚类系数 \(C(k)\), 网络直径 \(D\), 最短路径 \(d\), 平均路径长度 \(L\), 介数 \(B\), 点介数, 边介数, 网络介数, 核数, 中心性, 连通度, 结构熵, 特征谱

数理统计基础

分布函数变换

矩母函数 (Moment Generating Function, MGF)

\[ m_X(t) = E\left[e^{tX}\right], -\infin < t < h \]
  • 不是所有的分布都有矩母函数, 如 重脱尾的 Cauchy 分布
  • 对于部分 PDF 和 CDF 比较复杂的分布, 使用矩母函数可以大大降低复杂性.
  • 对于两个独立随机变量 \(X\) 和 \(Y\), 有 \(m_{X+Y}(t) = m_X(t)m_Y(t)\)

对矩母函数做 Taylor 展开, 得到:

\[ m_X(t) = \sum_{k=0}^{\infin}\frac{t^k}{k!}E[X^k] = 1 + tE[X] + \frac{t^2}{2!}E[X^2] + \frac{t^3}{3!}E[X^3] + \cdots \]

其中, \(E[X^k]\) 为 \(X\) 的 \(k\) 阶原点矩. 可以发现, 通过矩母函数, 可以得到 \(X\) 的所有原点矩.

\[ E[X^k] = \frac{\mathrm d^k}{\mathrm dt^k}m_X(t)\bigg|_{t=0} \]

注:

  • 原点矩: \(v_k(X) = E[X^k]\)
  • 中心矩: \(\mu_k(X) = E[(X - E[X])^k]\)

特征函数 (Characteristic Function)

\[ \varphi_X(t) = E\left[e^{itX}\right], -\infin < t < \infin \]
  • 分布函数与特征函数构成双射
  • 特征函数可以看成是 PDF 的 Fourier 变换
  • 特征函数是矩母函数在虚轴上取得, 即 \(\varphi_X(t) = m_X(it)\)

概率母函数 (Probability Generating Function, PGF)

对于在非负整数集上取值的离散随机变量 \(X\), 有概率母函数: $$ G_X(t) = E[t^X] = \sum_{k=0}^{\infin}t^kp(k) $$

  • 该式是一种 Z 变换的形式
  • 若 \(|t| \le 1\), 则 \(G_X(t)\) 收敛
  • 概率母函数是矩母函数在对数轴上取得, 即 \(G_X(t) = m_X(\ln t)\)

经典统计分布

\(\chi^2\) 分布

todo

注:

Gamma 函数: \(\Gamma(x) = \int_0^{\infin}t^{x-1}e^{-t}\mathrm dt\)

  • 当 \(x > 0\) 时, \(\Gamma(x)\) 收敛
  • \(\Gamma(x+1) = x\Gamma(x)\). 特别地, \(\Gamma(n+1) = n\Gamma(n) = \cdots = n!\Gamma(1) = n!\)
  • \(\Gamma(\frac{1}{2}) = \sqrt{\pi}\)

\(t\) 分布

todo

\(F\) 分布

todo

\(Gamma\) 分布

\[ f(x) = \frac{x^{\alpha - 1}e^{-\frac{x}{\beta}}}{\beta^\alpha\Gamma(\alpha)}, x > 0, \alpha > 0, \beta > 0 \\ E[X] = \alpha\beta, D[X] = \alpha\beta^2 \]

todo

统计检验方法

显著性水平

  • 以真为假: \(p = P\left\{\text{拒绝}H_0 | H_0 \text{成立}\right\}\)
  • 以假为真: \(\eta = P\left\{\text{接受}H_0 | H_0 \text{不成立}\right\}\)
  • 目标: 在保证 \(p\) 不超过临界值, 同时使 \(\eta\) 尽可能小

Q-Q 图 (Quantile-Quantile Plot)

Q-Q 图是一种用于比较两个概率分布的图形方法. 通过将两个概率分布的分位数相互对应, 从而比较两个概率分布的相似性.

todo

Kolmogorov-Smirnov 检验

todo

\(\chi^2\) 拟合优度检验

todo

矩阵理论

置换矩阵: 设 \(P\) 为一个 \(m\times n\) 维的 01 矩阵, 若 \(m \le n\) 且 \(PP^T=I\), 则称 \(P\) 为一个置换矩阵.

定理: 当 \(m \le n\) 时, \(P\) 为置换矩阵的充要条件是 \(P\) 的每一行恰有一个 1, 每一列恰有一个 1.

可约矩阵: 若存在一个置换矩阵 \(P\), 使得 \(PLP^T\) 为分块上三角阵, 则称 \(L\) 为可约矩阵, 否则称 \(L\) 为不可约矩阵.

定理: 矩阵 \(L\) 不可约等价于其对应的有向图是强连通的.

引理: 若 \(L=(a_{ij})_{N\times N}\) 是实对称不可约矩阵, 其中 \(a_{ij} \ge 0 (i\neq j)\), \(a_{ii} = \sum_{j=1,j\neq i}^N a_{ij}\), 则 - 0 是矩阵 \(L\) 的一个重特征值, 对应特征向量为 \([1, 1, \cdots, 1]^T\) - 矩阵 \(L\) 的其他特征值都小于 0 - 存在正交矩阵 \(\Phi = [\phi_1, \phi_2, \cdots, \phi_N]\), 使得 \(\Phi^T L \Phi = \Lambda = \mathrm{diag}(\lambda_1, \lambda_2, \cdots, \lambda_N)\), 即 \(L^T\phi_i = \lambda_i\phi_i\)

复杂网络特征的数学描述

静态几何特征

度 (Degree) 与 度分布 (Degree Distribution)

节点度: 节点 \(i\) 的度为 \(k_i\), 即与节点 \(i\) 相连的边的条数.

平均度: \(\langle k \rangle = \frac{1}{N}\sum_{i=1}^N k_i\)

度分布: \(P(k) = \frac{N_k}{N}\), 其中 \(N_k\) 为度为 \(k\) 的节点数.

无标度

许多真实网络的度分布可以用幂律分布来描述, 即 \(P(k) \propto k^{-\gamma}, \gamma \in (2, 3)\). 具有幂律度分布的网络称为无标度网络.

注:

无标度特性指: 属性特征与尺度变化无关. 考虑一个 PDF \(f(x)\), 无标度条件对应为 \(\forall a, \exist b, f(ax)=bf(x)\), 进而可以推得

\[ f(x) = f(1)x^{-\gamma}, \gamma =-\frac{f'(1)}{f(1)} \]

累积度分布 (Cumulative Degree Distribution)

\[ P_k = \sum_{i=k}^\infty P(i) \]

若 \(P(k) \propto k^{-\gamma}\), 则 \(P_k \propto k^{-(\gamma - 1)}\)

平均路径长度

todo

聚类系数

\[ C_i = \frac{2E_i}{k_i(k_i - 1)} = \frac{a_{ii}^{(3)}}{a_{ii}^{(2)}(a_{ii}^{(2)} - 1)} \]

无向网络静态特征

联合度分布 (Joint Degree Distribution)

联合度分布: \(P(k, k') = \frac{N_{kk'}}{N}\), 其中 \(N_{kk'}\) 为度为 \(k\) 和 \(k'\) 的节点对数.

度-度相关性

todo

聚类系数分布函数

聚-度相关性

局部聚类系数 \(C(k)\)

统计表示, 真实网络存在以下关系: \(C(k) \propto k^{-1}\). 具有该特性的网络称为层次网络.

介数

核数

中心性

度中心性

介数中心性

特征向量中心性

PageRank

Markov 链

赋权网络静态特征

其他静态特征

网络结构熵

\[ I_i = \frac{k_i}{\sum_{j=1}^N k_j} \\ E = -\sum_{i=1}^N I_i \ln I_i \]

网络特征谱

经典复杂网络模型

现实世界中的真实网络，一般都表现出小世界特性、无标度幂律分布、高聚类系数等特征

规则网络 (Regular Network)

网络中任意两个节点之间的联系遵循既定规则.

特征: 平移对称性, 每个节点的度和聚类系数相同, 聚类系数 C 大, 平均路径长度 L 长.

全局耦合网络 (Global Coupling Network, GCN)

任意两点之间都有边直接相连

GCN

\[ \begin{aligned} &\text{度分布:} \ P(k) = \delta(k - n + 1) \\ &\text{聚类系数:} \ C = C_i = 1 \\ &\text{平均路径长度:} \ L = L_{ij} = 1 \end{aligned} \]

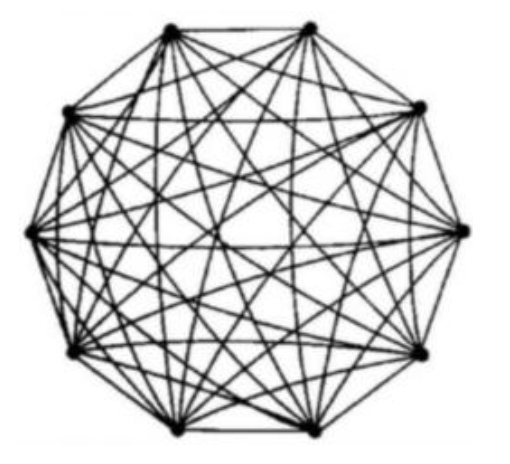
局限性: 实际复杂网络较稀疏, 边数为 \(O(n)\), 而非 \(O(n^2)\).

最近邻耦合网络 (Nearest Neighbor Coupling Network, NCN)

每个节点只与其最近邻的 \(K\) 个节点相连, 解决 GCN 的局限性

NCN

\[ \begin{aligned} &\text{度分布:} \ P(k) = \delta(k - K) \\ &\text{聚类系数:} \ C = C_i = \frac{\left(\frac{K}{2}-1\right)\left(\frac{K}{2}+1\right) + \Sigma_{i=0}^{\frac{K}{2}-2}i}{\frac{1}{2}K(K-1)} = \frac{3(K - 2)}{4(K - 1)} \\ &\text{平均路径长度:} \ L = L_{ij} = 1 \end{aligned} \]

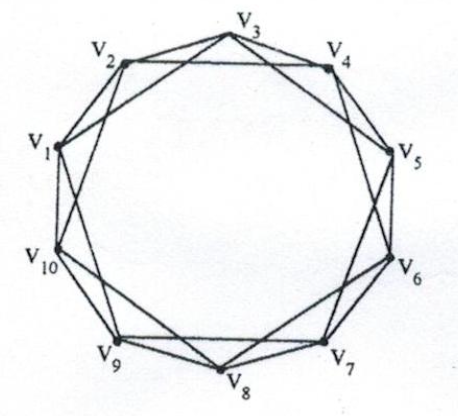
星形耦合网络 (Star Coupling Network, SCN)

随机网络

Erdos-Renyi 随机网络 (Erdos-Renyi Random Network, ERN)

若连接概率 \(p\) 大于某个临界值 \(p_c\), 则几乎每一个随机网络都是连通的

\[ p > p_c \propto \frac{\ln N}{N} \]
\[ \begin{aligned} &\text{平均度:} \ \langle k \rangle = p(N - 1) \approx pN \\ &\text{度分布:} \ P(k) = C_{N-1}^k p^k(1-p)^{n-k} \approx \frac{e^{-\langle k \rangle} \langle k \rangle^k}{k!} \\ &\text{直径:} \ D_{ER} = \frac{\ln N}{\ln \langle k \rangle} \approx \frac{\ln N}{\ln pN} \\ &\text{平均路径长度:} \ L_{ER} \propto \frac{\ln N}{\ln \langle k \rangle} \\ &\text{聚类系数:} \ C_{ER} = \frac{\langle k \rangle}{N - 1} \approx \frac{pN}{N} = p << 1 \end{aligned} \]

特征谱: todo

小世界网络 (Small World Network, SWN)

Watts-Strogatz 小世界网络 (Watts-Strogatz Small World Network, WSSWN)

随机化重连:

Newman-Watts 小世界网络 (Newman-Watts Small World Network, NWSWN)

随机化加边:

性质

\[ \begin{aligned} &\text{聚类系数:} \ C_{WS}(p) = \frac{3(K - 2)}{4(K - 1)}(1 - p)^3, C_{NW}(p) = \frac{3(K - 2)}{4(K - 1) + 4K(p+2)} \\ \end{aligned} \]

特征谱

无标度网络 (Scale-Free Network, SFN)

度分布服从幂律分布的网络, \(P(k) \propto k^{-\gamma}\), 其中 \(\gamma\) 通常在 2 到 3 之间.

Barabasi-Albert 无标度网络 (Barabasi-Albert Scale-Free Network, BASFN)

  1. 增长特性
  2. 优先连接
\[ \Pi_i = \frac{k_i + 1}{\Sigma_j (k_j + 1) } \]
最后更新: November 16, 2023
创建日期: November 3, 2023